There Are No Words Powerful Enough To Express The Importance of Basic Scientific Research
Galileo's Theory of  the Pendulum was flawed but! (ref. 1)
by
Jim & Rhoda Morris      781 245 2897    SciTechAntiques.com    K1ugm@comcast.net

This page is not just about building and demonstrating the importance's of the Cycloid Curve in making more accurate clocks but also gives a clearer vision about basic research in the 1600's
 

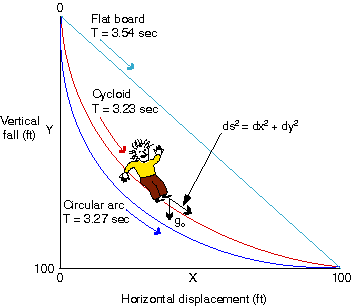
It  gives us a  demonstration of   team work in basic scientific research and shows how a causal observation of some swinging chandeliers coupled with the application of the techniques of basic research led to a seed of knowledge which gave us accurate time keeping devices. This gave scientist one of the three basic measurements that are so vital to all research in the natural sciences   TIME.  The other two are LENGTH, and  MASS.  

Galileo's simple model of the pendulum was too simple, its circular path  did not keep perfect time.  The pendulum path should  have followed a cycloid curve. A curve that could only be derived for  a pendulum through the application of a mathematical approach not an experimental approach.  See example  It used the physics of force fields. Gravity in this case. Again, the curve is called the cycloid.

 Just for the record, the shortest time between two points is not always a straight line. This can be shown with the apparatus described further on in this page.



Click here To See  What Galileo's Telescopes Looked When New and Their  Surprising Construction.
Click here  HISTORICAL INSTRUMENTS OF SCIENCE & TECHNOLOGY FOR SALE & FOR PROPS
  

A short history and description of the cycloid
A Cycloid Curve is generated by a point on a circle's circumference rolling on a plane. See figures below.  The cycloid posses interesting physical properties. It is brachistochronous and tautochronous: brachistochronous, because it represents the path completed in the shortest time between two points for a given type of motion (such as a fall under the effect of gravity); tautochronous, because a body made to oscillate along a cycloid will always take the same time to cover it, whatever the amplitude of the oscillation. Galileo (1564-1642) mistakenly believed circular oscillations to be tautochronous. The brachistochronous property of the cycloid was demonstrated by Jacques Bernoulli (1654-1705) in 1697, while Christiaan Huygens (1629-1695) proved its tautochronism in 1659.

Looking at the curve below one can see that there is only 4 hundreds of a second different between the path taken running on a circle and  a cycloid. Perhaps Galileo can be forgiven for missing this small difference?

Perhaps not, If Galileo had been a sharper theoretical physicist and less of an experimental physicist  he might have beat Christiaan Huygens to the discovery of the cycloid curve and a  truly tautochronous pendulum.

The bottom line; The trouble is very very few scientist are good at  both theory and experiment. A typical scientist is either good at one or the other. In the end, it is always a team of scientist each adding their own unique specialty to completely explain a natural phenomena.

In spite of what the media inspired public would have you believe No one scientist is an island unto himself.

 (ref. 1)  http://brunelleschi.imss.fi.it/catalogo/genappr.asp?appl=SIM&xsl=approfondimento&lingua=ENG&chiave=100077

Below diagrams  and photos of the mechanical generation of a cycloid curve and the tool used to do it.



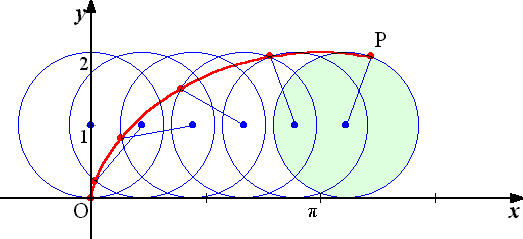
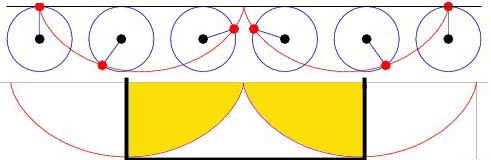
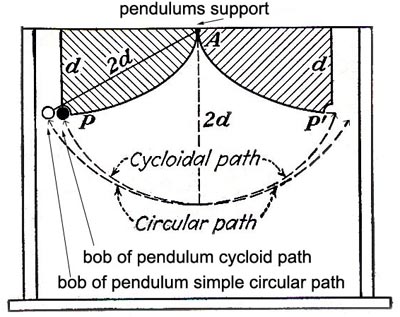
See example of the movement of the pendulum constrained to a cycloid curve

The not so simple Galileo's pendulum.

Two  pieces in wood, metal, or plastic shaped in the form of a cycloid may be  inverted to form a cusp, between these sides a simple pendulum may be made to oscillate with  a cycloid path with a large or small amplitude  (Fig.  24.  Direct comparison with the added simple pendulum of the same length but without the cycloid attachment shows that the span style cycloidal pendulum is isochronous, regardless of amplitude. On the other hand the simple pendulum period  depends upon the amplitude of its swing.  If both pendulums are swung through large arcs, the cycloidal pendulum gains on the simple pendulum.

 

The following site gives a mathematical derivation of the cycloid;      http://mathworld.wolfram.com/TautochroneProblem.html http://mathworld.wolfram.com/Cycloid.html

 

Building an Apparatus to Demonstrate Some of the Properties of the Famous Cycloid Curve
This is a very rare view  of science seldom if ever seen by the public. It's from the instrument maker's perspective, those unsung heroe's behind the great scientist work.
 

This instrument is in the Museum of History of Science of Florence Italy (inv. 969) We made some alteration to this design. They are listed below.

http://brunelleschi.imss.fi.it/genscheda.asp?appl=LST&xsl=approfondimento&lingua=ENG&chiave=704014


 .
 

To demonstrate the above properties of a cycloid we built an apparatus that consists of  two cycloid tracks and an adjustable incline plane.  The two tracks for the cycloid demonstrate the tautochronous effect:  two balls falling from different heights down each track will arrive at the bottom at the same time.  The combination of a cycloid track and the incline plane demonstrate the brachistochronous effect:  for two balls falling from the same height on each, the ball falling down the cycloid will reach the bottom of the curve before the ball falling down the incline plane even though the ball falling down the plane travels a shorter distance.

Click on the thumbnails below to get a larger picture
cyc1 cyc2 cyc3
Step one: making a
cycloid generating wheel
cyc1.jpg 		Step two: generating
a cycloid curve
cyc2.jpg 		Close up of step two
cyc3.jpg
cyc4 cyc5 cyc6

 
Cutting out the cycloid
curve on two sheets of
furniture grade plywood that
have been temporally
fastened together
cyc4.jpg 		legs have been added and The first rough
tests are under way.
cyc5.jpg 		Adding the two tracks
cyc6.jpg



Above and below we  added the adjustable inclined plane and some decorations to make it attractive for people to use and also to give  the cycloid curve the recognition it deserves.

THE PLUM BOB  FOR LEVELING THE APPARATUS

 
THE END OF THE LINEAR INCLINED
TRACK


THE TOP OF THE  INCLINED PLANE AND STORAGE CUPS FOR THE BALLS


BELOW THE FINAL VERSION  OF THE APPARATUS

Below; The bottom line!
An experimentalist beginning the testing of Galileo's theory with the apparatus. Which ball will get to the bottom first? Will both balls keep the same  period regardless of the amplitude of their  swing?

Below a 56 sec video showing the  tautochronous nature of our cycloid shaped rail apparatus.
To play video place the curser in the center of the frame below.

Below a 46 sec video showing the  brachistochronous nature of our cycloid shaped rail apparatus.
To play video place the curser in the center of the frame below.


 

8/11/2005

Hit Counter
Copyright  8/8/2005by Jim & Rhoda Morris/font>